https://www.acmicpc.net/problem/2839
2839번: 설탕 배달
상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그
www.acmicpc.net
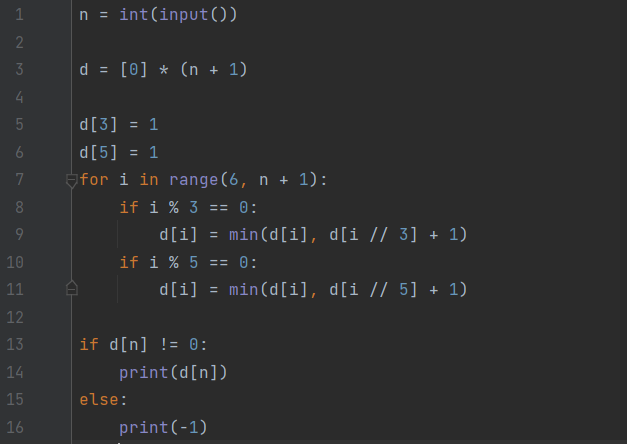
다이나믹 프로그래밍 문제를 풀다보니 문제를 보자마자 Bottom-up 방식으로 접근했는데, 다른 풀이들을 찾아보니 꼭 다이나믹 프로그래밍을 사용하지 않아도 된다는 걸 깨달았다.
알고리즘 분류를 확인해보니

이렇기에
너무 문제 푸는거에 집중하다보니
실제 코테에서는 문제를 보고 어떤 방식으로 접근해야 하는지부터 나 스스로 생각해내야 하는데, 내가 지금 공부하는 부분이니까 당연히 그 방식으로 접근하고 있는(+예제 참고) 안좋은 모습을 발견했다.
그래서 든 생각
"다이나믹 프로그래밍(동적 계획법)과 그리디 알고리즘의 차이는 뭘까? 그리고 각각 어떤 경우에 적용하는게 좋은지?"
이거에 관해서는 다음 포스팅의 앞부분에서 짧게 다루고 있으니 참고하면 좋을 것 같다.
https://pingzeming.tistory.com/49
다이나믹 프로그래밍(DP, 동적 계획법)의 특징
이번 포스팅은 오랜만에 알고리즘 관련임 음하하 교재의 예제들과 함께 백준의 #1463 문제를 풀면서 오랜만에 문제 풀이 포스팅을 적으려다가 어쩌다보니 방향이 바뀌어버려서 글 흐름이 조금
pingzeming.tistory.com
다이나믹 프로그래밍을 다시 공부하면서 이전에 해결하지 못하고 미뤘던 이 문제를 지금에서야 다시 풀게 됐다.
다시 보니 해당 문제는 그리디로 풀기에 적절하지 않고, 누가 봐도 동적 계획법을 사용하면 되는 문제임을 알 수 있었다...
그전엔 도대체 뭘 공부한건지 민망할 정도이다.ㅋ..
이전에 풀다 만 풀이에서 수정하지 않고, 그냥 다시 처음부터 스스로 풀어보았다.
우리는
1) 5kg짜리 또는 3kg짜리 봉지를 사용할 수 있고,
2) 두 가지 중 어떤 것을 사용하든 가장 최소한으로 사용해야 한다
는 것을 고려하면,
d[i]는 d[i - 5]와 d[i -3]의 값과 관련이 있을 수밖에 없고, 이를 바탕으로 점화식으로 세울 수 있다.
예시에 나온 18을 가지고 그림을 그려보니
금방 패턴을 찾을 수 있었다.
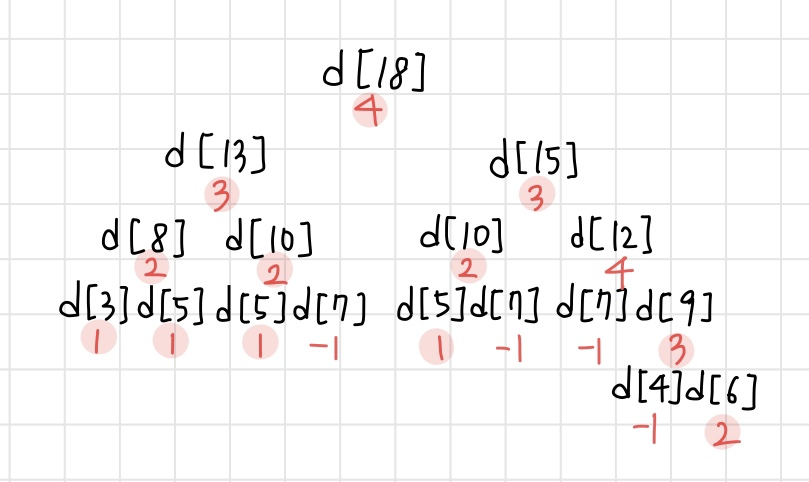
-1이라는 값은 n=3 부터 n=7 까지는 나올 수 있으나 그 이후부터는 나오지 않기에 평소보다 조금 오버해서 d[7]까지의 값을 미리 초기화해주었다.
그리고 d[i - 5]와 d[i - 3] 중 -1이 나오는 경우를 제외하고는 d[i - 5]와 d[i -3] 중 더 작은(사용한 봉지의 개수는 최소가 되어야 하므로) 값에서 1을 더한 값이 d[i]의 값이 되는 것을 알 수 있다.
반면에 d[i - 5] 또는 d[i -3] 중 하나가 -1인 경우에는 3과 5로 더해서 만들 수 없는 경우이기 때문에 아예 버려두고 -1이 아닌 것을 선택(무조건 -1보다는 클 수밖에 없기에 max 함수를 사용하여 선택)하도록 하여 코드를 작성해주었다.
n = int(input())
d = [0] * 5001
d[3] = 1
d[4] = -1
d[5] = 1
d[6] = 2
d[7] = -1
for i in range(8, n + 1):
if d[i - 5] != -1 and d[i - 3] != -1:
d[i] = min(d[i - 5] + 1, d[i - 3] + 1)
else:
d[i] = max(d[i - 5] + 1, d[i - 3] + 1)
print(d[n])
'알고리즘 > 백준 풀이' 카테고리의 다른 글
| [백준/Python] #20115 : 에너지드링크 - 그리디 (0) | 2023.07.20 |
|---|---|
| [백준/Python] #1343 : 폴리오미노 - 그리디 (0) | 2023.07.20 |
| [백준/Python] #9095 : 1, 2, 3 더하기 - 다이나믹 프로그래밍 (0) | 2023.05.25 |
| [백준/Python] #1920 : 수 찾기 - 이분탐색 (0) | 2023.05.18 |
| [백준/Python] #2309 : 일곱 난쟁이 (0) | 2023.05.18 |
https://www.acmicpc.net/problem/2839
2839번: 설탕 배달
상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그
www.acmicpc.net

다이나믹 프로그래밍 문제를 풀다보니 문제를 보자마자 Bottom-up 방식으로 접근했는데, 다른 풀이들을 찾아보니 꼭 다이나믹 프로그래밍을 사용하지 않아도 된다는 걸 깨달았다.
알고리즘 분류를 확인해보니

이렇기에
너무 문제 푸는거에 집중하다보니
실제 코테에서는 문제를 보고 어떤 방식으로 접근해야 하는지부터 나 스스로 생각해내야 하는데, 내가 지금 공부하는 부분이니까 당연히 그 방식으로 접근하고 있는(+예제 참고) 안좋은 모습을 발견했다.
그래서 든 생각
"다이나믹 프로그래밍(동적 계획법)과 그리디 알고리즘의 차이는 뭘까? 그리고 각각 어떤 경우에 적용하는게 좋은지?"
이거에 관해서는 다음 포스팅의 앞부분에서 짧게 다루고 있으니 참고하면 좋을 것 같다.
https://pingzeming.tistory.com/49
다이나믹 프로그래밍(DP, 동적 계획법)의 특징
이번 포스팅은 오랜만에 알고리즘 관련임 음하하 교재의 예제들과 함께 백준의 #1463 문제를 풀면서 오랜만에 문제 풀이 포스팅을 적으려다가 어쩌다보니 방향이 바뀌어버려서 글 흐름이 조금
pingzeming.tistory.com
다이나믹 프로그래밍을 다시 공부하면서 이전에 해결하지 못하고 미뤘던 이 문제를 지금에서야 다시 풀게 됐다.
다시 보니 해당 문제는 그리디로 풀기에 적절하지 않고, 누가 봐도 동적 계획법을 사용하면 되는 문제임을 알 수 있었다...
그전엔 도대체 뭘 공부한건지 민망할 정도이다.ㅋ..
이전에 풀다 만 풀이에서 수정하지 않고, 그냥 다시 처음부터 스스로 풀어보았다.
우리는
1) 5kg짜리 또는 3kg짜리 봉지를 사용할 수 있고,
2) 두 가지 중 어떤 것을 사용하든 가장 최소한으로 사용해야 한다
는 것을 고려하면,
d[i]는 d[i - 5]와 d[i -3]의 값과 관련이 있을 수밖에 없고, 이를 바탕으로 점화식으로 세울 수 있다.
예시에 나온 18을 가지고 그림을 그려보니
금방 패턴을 찾을 수 있었다.
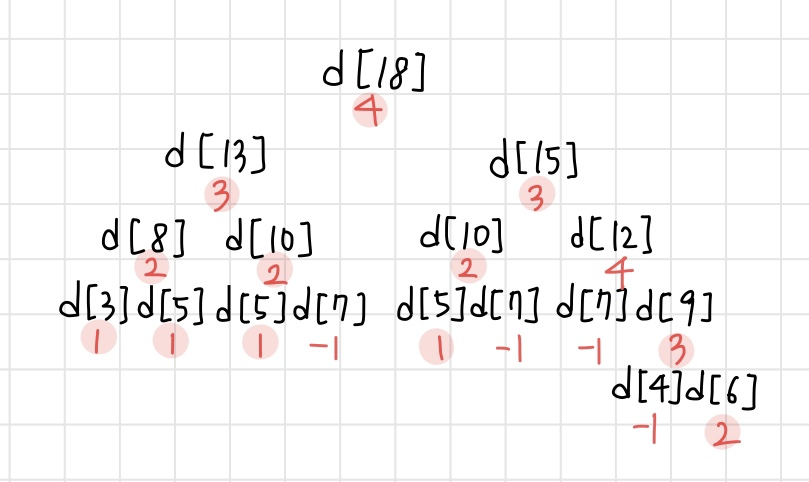
-1이라는 값은 n=3 부터 n=7 까지는 나올 수 있으나 그 이후부터는 나오지 않기에 평소보다 조금 오버해서 d[7]까지의 값을 미리 초기화해주었다.
그리고 d[i - 5]와 d[i - 3] 중 -1이 나오는 경우를 제외하고는 d[i - 5]와 d[i -3] 중 더 작은(사용한 봉지의 개수는 최소가 되어야 하므로) 값에서 1을 더한 값이 d[i]의 값이 되는 것을 알 수 있다.
반면에 d[i - 5] 또는 d[i -3] 중 하나가 -1인 경우에는 3과 5로 더해서 만들 수 없는 경우이기 때문에 아예 버려두고 -1이 아닌 것을 선택(무조건 -1보다는 클 수밖에 없기에 max 함수를 사용하여 선택)하도록 하여 코드를 작성해주었다.
n = int(input())
d = [0] * 5001
d[3] = 1
d[4] = -1
d[5] = 1
d[6] = 2
d[7] = -1
for i in range(8, n + 1):
if d[i - 5] != -1 and d[i - 3] != -1:
d[i] = min(d[i - 5] + 1, d[i - 3] + 1)
else:
d[i] = max(d[i - 5] + 1, d[i - 3] + 1)
print(d[n])
'알고리즘 > 백준 풀이' 카테고리의 다른 글
| [백준/Python] #20115 : 에너지드링크 - 그리디 (0) | 2023.07.20 |
|---|---|
| [백준/Python] #1343 : 폴리오미노 - 그리디 (0) | 2023.07.20 |
| [백준/Python] #9095 : 1, 2, 3 더하기 - 다이나믹 프로그래밍 (0) | 2023.05.25 |
| [백준/Python] #1920 : 수 찾기 - 이분탐색 (0) | 2023.05.18 |
| [백준/Python] #2309 : 일곱 난쟁이 (0) | 2023.05.18 |
